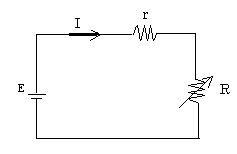
(H10電験3種理論)
図のような直流回路において、R=10[Ω]のときはI=5[A]であり、R=8[Ω]のときはI=6[A]であった。この場合、電源電圧E[V}の値として、正しいのは次のうちどれか。

[ ① 35 ② 40 ③ 48 ④ 50 ⑤ 60 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
題意より E=5(r+10)----① E=6(r+8) ----②
①、②より5(r+10)=6(r+8) ゆえにr=2(Ω)
これを②に代入するとE=60 (V) 解答⑤
(H15電験3種理論)
図のような直流回路において、電源電圧がE[V]であったとき、端末の抵抗の端子間電圧の大きさが1[V]であった。このときの電源電圧E[V]の値として、正しいのは次のうちどれか。
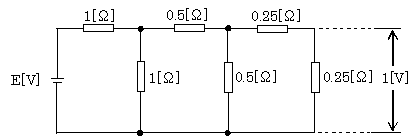
① 34 ② 20 ③ 14 ④ 6 ⑤ 4
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
右端の抵抗と直列の0.25Ωの抵抗に加わる電圧は、1V×2より2Vとなる。
この合成抵抗は025+025=0.5Ω であり、左の抵抗0.5Ωと並列回路になるので、合成抵抗は0.25Ωで、電圧は2Vとなる。この抵抗とR1は直列回路で、合成抵抗は0.75Ωで、電圧は6Vとなる。この抵抗とR2は並列回路となり、合成抵抗は3/7Ωとなり、電圧が6Vとなる。
ここにおいて。R3と3/7は直列回路であり、次式が成り立つ。
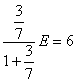
これをEについて解くと、 E=20 (V) 解答 ②
(H13電験3種理論)
図のような直流回路において、電源を流れる電流は、100[A]であった。このとき、80[Ω]の抵抗に流れる電流I[A]の値として、正しいのは次のうちどれか。
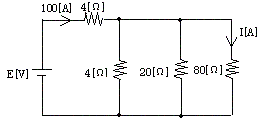
① 3 ② 4 ③ 5 ④ 6 ⑤ 7
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
80Ωと20Ωは並列回路であるため、20Ωに流れる電流をI1とすると、電圧が等しいことから次式が成立する。
I1×20=I×80 ゆえに I1=4I
また、この並列回路の合成抵抗は20×80/(20+80)=16 Ω となり、電流は4I+I=5Iとなる。
16Ωと4Ωは並列回路であり、4Ωに流れる電流をI2とすると次式が成立する。
I2×4=5I×16 ゆえに I2=20I
ゆえにこの合成電流は5I+20I=25I 題意より25I=100 (A) なので、
I=4 (A) 解答 ②
(H9電験3種理論)
図のような回路において、抵抗R[Ω]の値として、正しいのは次のうちどれか。
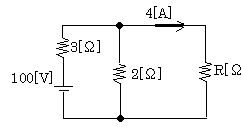
[ ① 2.2 ②4.0 ③8.8 ④10.3 ⑤15.5 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
3Ωに流れる電流をIとすると次の関係式が成立する。
100=3I+4R----① (4Rは、並列回路のRの電圧)
I=4+4R/2=4+2R----② (4R/2は、並列回路の抵抗2Ωに流れる電流)
①に②を代入してRを解く。
100=3(4+2R)+4R
10R=88 ゆえに R=8.8 (Ω) 解答 ③
(H14電験3種理論)
図1の抵抗回路において、抵抗R[Ω]の消費する電力は72[W]である。このときのpq端子の電圧V[V]をもとめる。次の(a)及び(b)に答よ。
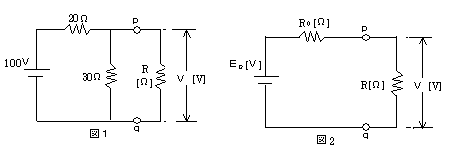
(a) 図1のpq端子から左側を見た回路は図2に示すように、電圧源E0[V]と内部抵抗R0[Ω]の電源回路に置き換えることができる。E0[V]とR0[Ω]の値として、正しいのは次のうちどれか。
① 40 6 ② 60 12 ③ 100 20 ④ 60 30 ⑤ 40 50
(b) 抵抗R[Ω]が72[W]を消費するときのR[Ω]の値には二つある。それぞれに対応した電圧V[V]のうち、高い方の電圧V[V]の値として正しいのはどれか。
① 36 ② 50 ③ 72 ④ 84 ⑤ 100
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
鳳・テブナンの定理を利用するのがポイント。
(a)pq端子から左側を見た内部抵抗R0[Ω]は、電圧源を短絡した回路構成となる。つまり、抵抗20Ωと抵抗30Ωの並列回路となるので、R0=20×30/(20+30)=12 Ω また、電圧は、電圧源100Vと抵抗20Ωと抵抗30Ωの直列回路となるので、E0=100×30/(20+30)=60 (V) 解答 ②
(b)Rに流れる電流をIとすると、鳳・テブナンの定理により、
I=60/(12+R)となる。また消費電力はRI2で、題意よりこれが72[W]なので、
72=R×602/(12+R)2
これをRについて解く。
R2+24R+144=50R R2-26R+144=0
(R-8)(R-18)=0 ゆえに R=8 or 18
R=8のときはI=3 そのときの電圧は24V
R=18のときはI=2 そのときの電圧は36V
高い方の電圧は36Vである。 解答 ①
(H13電験3種理論)
図の回路において、スイッチSを閉じた瞬間(時間=0)に抵抗R1に流れる電流をI0[A]とする。また、スイッチSを閉じた後、回路が定常状態に達したとき、同じ抵抗R1に流れる電流I∞[A]とする。上記の電流I0及びI∞の値の組み合わせとして、正しいのは次のうちどれか。
|
|
|
I0 |
I∞ |
|
① |
|
|
|
|
② |
|
|
|
|
③ |
|
|
|
|
④ |
|
||
|
⑤ |
|
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
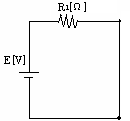
①スイッチSを閉じた瞬間は、コンデンサが電気的に短絡状態となる。そのため
下図の等価回路になる。ゆえに I0=E/R1
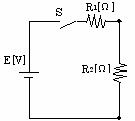
②スイッチSを閉じて、定常状態に達したときは、コンデンサが電気的に開放状態となる。そのため下図の等価回路になる。
ゆえに I∞=E/(R1+R2)
 解答 ④
解答 ④
(H12電験3種理論)
図の直流回路において、電源を流れる電流I[A]の値として、正しいのは次のうちどれか。
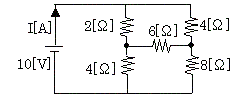
①1.0 ② 1.5 ③ 2.0 ④ 2.5 ⑤ 3.0
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
上図の回路はブリッチ回路であり、対角線上の抵抗値の積が等しいので、6Ωの抵抗には電流が流れず、電気的には開放状態と同等である。すなわち下図の等価回路となる。
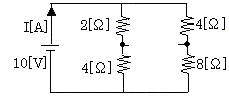
上回路の合成抵抗をRとすると、
![]()
解答 ④
(H10電験3種理論)
図のような回路において、端子ab間の合成抵抗[Ω]の値として、正しいのは次のうちどれか。
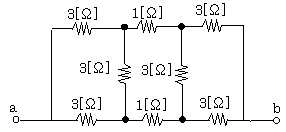
[ ①2.5 ②3.0 ③ 3.5 ④ 4.0 ⑤4.5 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
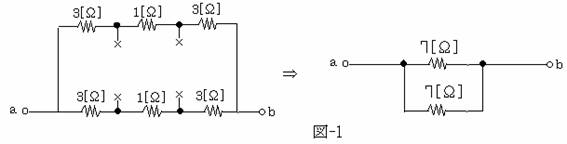
上図において同じ抵抗値で並列回路が構成されているので、3[Ω]の両端の電位は等しく電流が流れないので、電気的に開放された状態と同等である。
よって、図1のような回路に変換し簡略化することが出来る。7Ωの並列回路であるため、合成抵抗は3,5Ωとなる。 解答 ③
(H11電験3種理論)
図のL及びCを含む直流回路において、L及びCに蓄えられるエネルギーの合計値[J]として、正しいのは次のうちどれか。
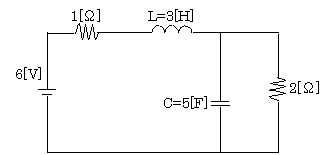
[ ① 6 ② 30 ③ 46 ④ 54 ⑤ 80 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
電源が直流なので、定常状態ではLは短絡状態であり、Cは開放状態となる。つまり下図のような等価回路となり、回路に流れる電流I(Lに流れる電流と同じ)とし、抵抗2Ωに加わる電圧をV(Cの充電電圧と同じ)とすると、
![]()
また、Lに蓄えられるエネルギーをW1、Cに蓄えられるエネルギーをW2とすると、公式により
![]()
![]()
H10電験3種理論
二つの抵抗R1[Ω]及びR2[Ω]を図1のように並列に接続した場合の全消費電力は、これら二つの抵抗を図2にように直列に接続した場合の全消費電力の6倍であった。このとき、R2の値として、正しいものは次のうちどれか。ただし、R1=1[Ω]、R2>R1とし、電源Eの内部抵抗は無視するものとする。
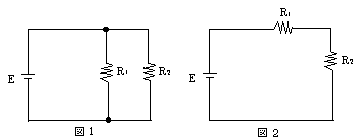
[ ① 1.1 ② 1.4
③ 2.0 ④ 3.7 ⑤ 4.3 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解説および解答
図1の消費電力をP1、図2の消費電力をP2とすると
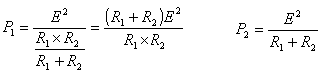
題意より、P1=6P2なので
![]()
R1=1を代入してR2について解くと、
![]()
![]()
ゆえにR2=0.3 or 3.7 題意よりR2>R1なので、 R2=3.7(Ω)
解答 ④