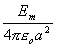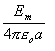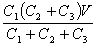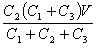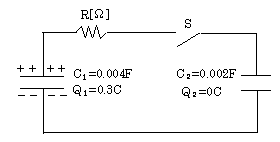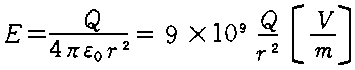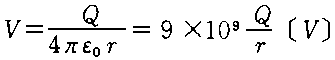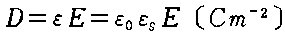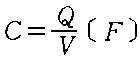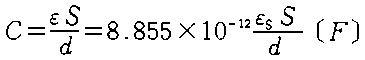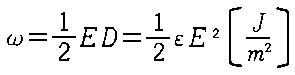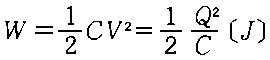گأ“d‚ة‚آ‚¢‚ؤ
(•½گ¬‚W”N“dŒ±‚Rژيپ@—ک_ڈo‘èپj
گ^‹َٹا‚ة‚p‚Pپپ‚S[ƒت‚b]‹y‚ر‚p‚Qپپ‚T[ƒت‚b]‚ج“ٌ‚آ‚ج“_“d‰×‚ھ‚S‚O[‚ƒ‚چ]—£‚ê‚ؤ‚ ‚é‚ئ‚«پA
“ٌ‚آ‚ج“_“d‰×‚جٹش‚ة“‚—ح‚ج‘ه‚«‚³[‚m]‚ح‚¢‚‚ç‚©پBگ³‚µ‚¢’l‚ًژں‚ج‚¤‚؟‚©‚ç‘I‚×پB
پ@پ@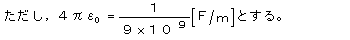 پ@پ@
پ@پ@
پ@پ@پi‚Pپj‚PپD‚P‚Rپ@پ@ پi‚Qپj‚PپD‚R‚Sپ@پ@ پi‚Rپj‚QپD‚S‚Tپ@پ@ پi‚Sپj‚RپD‚U‚Vپ@ پi‚Tپj‚SپD‚X‚U
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پ@پ@پڑ–â‘è‰ً“ڑ‹y‚ر‰ًگàپEپEپEپEپ@’Pˆت‚ة’چˆس‚µ‚ـ‚µ‚ه‚¤پBƒNپ[ƒچƒ“‚ة‚¨‚¢‚ؤƒت‚b‚ح10‚جƒ}ƒCƒiƒX‚UڈوCپA
پ@پ@‹——£‚S‚O[‚ƒ‚چ]‚ح0.4‚چ‚ة’Pˆت‚ً’²گ®‚µ‚ؤŒِژ®‚ة‘م“ü‚·‚ê‚خ“ڑ‚¦‚ھڈo‚ـ‚·پBگ³‰ً‚ح(1)
پiƒNپ[ƒچƒ“‚ج–@‘¥‚ج•â‘«گà–¾پj
“d‰×‚p1‚ئ‚p2‚ھ‹——£‚’‚¾‚¯—£‚ê‚ؤ”z’u‚³‚ê‚ؤ‚¢‚é‚ئپC—¼“d‰×‚جٹش‚ة‚حƒNپ[ƒچƒ“—ح‚ئŒؤ‚خ‚ê‚é—ح‚ھگ¶‚¶‚ـ‚·پB
‚±‚ج‚±‚ئ‚حچ‚چZ“™‚ج•¨—‚إٹù‚ةڈK‚ي‚ê‚ؤ‚¢‚é‚ئژv‚¢‚ـ‚·پBچ،‚àٹo‚¦‚ؤ‚¢‚ـ‚·‚©پHپ@
‚±‚ê‚ح“dŒ±‚Rژي‚ج—ک_‚ة‚¨‚¢‚ؤٹî‘b’†‚جٹî‘b‚إ‚ ‚èپAٹF—l‚ح“d‹C‚جگê–ه‰ئ‚ب‚ج‚إپAٹmژہ‚ةٹo‚¦‚ـ‚µ‚ه‚¤پB
ƒNپ[ƒچƒ“‚ج–@‘¥‚ح—ِˆ¤‚ج–@‘¥‚ةژ—‚ؤ‚¢‚ـ‚·پB—ح‚ًF‚ئ‚·‚é‚ئپAF‚حژںژ®‚ج‚و‚¤‚ة‚ب‚è‚ـ‚·پB
—ِˆ¤‚جژ‘±—ح‚حپA“ٌگl‚ج‚»‚ꂼ‚ê‚جژv‚¢‚جگدپi“d‰×‚p1‚ئ‚p2‚جگدپj‚ة”ن—ل‚µپA
“ٌگl‚ًٹu‚ؤ‚é‹——£پi‚’پj‚ج“ٌڈو‚ة”½”ن—ل‚µ‚ـ‚·پB
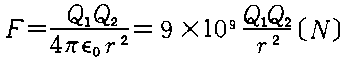
‚eپ@پ@پF“ٌ‚آ‚ج“d‰×‚ة“‚—ح [‚m]
Q1.Q2پF“ٌ‚آ‚ج“d‰×‚ج‚»‚ꂼ‚ê‚ج“d‹C—ت[C]
‚’پ@پ@پF“ٌ‚آ‚ج“d‰×ٹش‚ج‹——£[m]
ƒأoپ@پFگ^‹َ‚ج—U“d—¦[F/m]=8.855پ~10-12
(•½گ¬16”N“dŒ±‚Rژيپ@—ک_ڈo‘èپj
ژں‚ج•¶ڈح‚حپA“dٹE‚ئ“dˆتچ·‚جٹضŒW‚ة‚آ‚¢‚ؤڈq‚ׂ½‚à‚ج‚إ‚ ‚éپB‹Lڈq’†‚ج‹َ”’‰سڈٹ(پ@ƒAپ@)پA(پ@ƒCپ@)‹y‚ر(پ@ƒEپ@)‚ة“–‚ؤ‚ح‚ـ‚éŒê‹ه–”‚ح‹Lچ†‚ئ‚µ‚ؤپAگ³‚µ‚¢‚à‚ج‚ً‘g‚فچ‡‚ي‚¹‚½‚à‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
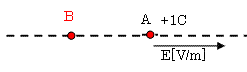
گ}‚ج‚و‚¤‚ةپA“dٹE‚ج‹‚³‚ھE[V/m]‚جˆê—l‚ب“dٹE’†‚ج“_A‚ةپA1[C]‚جگ³‚ج“_“d‰×‚ً‚¨‚‚ئپA‚±‚ج“_“d‰×‚ة‚ح(پ@پ@ƒAپ@پ@)‚ھ“‚پB‚¢‚ـپA‚±‚ج(پ@پ@ƒAپ@پ@)‚ة‹t‚ç‚ء‚ؤپA‚»‚ج“dٹE’†‚ج‘¼‚ج“_B‚ةپA‚±‚ج“_“d‰×‚ًˆع“®‚·‚é‚ة‚حٹO•”‚©‚çژdژ–‚ً‚µ‚ؤ‚â‚ç‚ب‚¯‚ê‚خ‚ب‚ç‚ب‚¢پB‚±‚ج‚و‚¤‚بڈêچ‡پA“_B‚ح“_A‚و‚è“dˆت‚ھ(پ@پ@ƒCپ@پ@)‚ئ‚¢‚¢پA“_A‚ئ“_B‚جٹش‚ة‚ح“dˆتچ·‚ھ‚ ‚é‚ئ‚¢‚¤پB“dˆتچ·‚ج‘ه‚«‚³‚حپA“_“d‰×‚ًˆع“®‚·‚é‚ئ‚«‚ة—v‚µ‚½ژdژ–‚ج‘ه‚«‚³‚ة‚و‚ء‚ؤŒˆ‚ـ‚èپAژdژ–‚ھ1[(پ@پ@ƒEپ@پ@)]‚ج‚ئ‚«پA2“_ٹش‚ج“dˆتچ·‚ح1[V]‚إ‚ ‚éپB
پ@
پ@پ@پ@پ@پ@پ@(پ@ƒAپ@)پ@پ@ (پ@ƒCپ@)پ@پ@پ@ (پ@ƒEپ@)
پ@پ@پ@پ@‡@ ‹N“d—ح پ@پ@پ@’ل‚¢پ@پ@پ@پ@پ@ C
پ@پ@پ@پ@‡A گأ“d—ح پ@پ@پ@چ‚‚¢ پ@پ@پ@پ@پ@J
پ@پ@پ@پ@‡B ‹N“d—حپ@پ@پ@ چ‚‚¢پ@پ@پ@پ@پ@ C
پ@پ@پ@پ@‡C •غژ—ح پ@پ@پ@’ل‚¢پ@پ@پ@پ@پ@ J
پ@پ@پ@پ@‡D گأ“d—ح پ@پ@پ@’ل‚¢پ@پ@پ@پ@پ@ N
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ–â‘è‰ً“ڑ‹y‚ر‰ًگàپEپEپEپE‚ ‚é“dٹE’†‚ة“_“d‰×‚ً‚¨‚‚ئگأ“d—حپiƒNپ[ƒچƒ“—حپj‚ھ“‚«‚ـ‚·پB
F=Qپ~E‚جژ®‚ة‚¨‚¢‚ؤپAQپپ‚P‚إ‚ ‚邽‚كپAE(N)‚جگأ“d—ح‚ھ“‚پBگأ“d—ح‚ة‹t‚ç‚ء‚ؤ“d‰×‚ًˆع“®‚³‚¹‚é‚ئپA“d‰×ٹش‚ج‹——£‚ھڈ¬‚³‚‚ب‚é‚ج‚إپA‘ه‚«‚بگأ“d—ح‚ھ”گ¶‚·‚éپBE=F/Q‚جژ®‚ج‚و‚¤‚ةپA“dˆت‚حگأ“d—ح‚ة”ن—ل‚·‚é‚ج‚إپAگأ“d—ح‚ھ‘ه‚«‚‚ب‚é‚ئ“dˆت‚àچ‚‚‚ب‚éپB“_“d‰×‚ًˆع“®‚µ‚½‚ئ‚«‚ة—v‚µ‚½ژdژ–‚ج‘ه‚«‚³‚حJپiƒWƒ…پ[ƒ‹پj‚ئ‚ب‚è‚ـ‚·پBڈعچׂح‚RپD“dˆت•â‘«گà–¾‚ًژQڈئپ@
گ³‰ً‡A
پi“dٹE‚ج‹‚³‚ج•â‘«گà–¾پj
‚ ‚镨‘ج‚ھ“d‰×‚ًژ‚آ‚ئپAژü‚è‚ج‹َٹش‚ة•¨—“Iڈَ‹µ•د‰»‚ً‚à‚½‚炵‚ـ‚·پB‚±‚ê‚ً“dڈê‚ـ‚½‚ح“dٹE‚ئŒ¾‚¢‚ـ‚·پB‚»‚µ‚ؤ‚±‚ج“dٹE‚ج’†‚ة‘¼‚ج“d‰×‚ًژ‚ء‚ؤ‚‚é‚ئپAگأ“d—حپiƒNپ[ƒچƒ“—حپj‚ھگ¶‚¶‚ـ‚·پB“dٹE‚ج‹‚³‚ج’è‹`‚حپA“_“d‰×‚©‚ç‹——£‚’‚ة’Pˆت“d‰×‚P[C]‚ًژ‚ء‚ؤ‚«‚½‚ئ‚«”گ¶‚·‚éگأ“d—ح‚ئ‚µ‚ؤچl‚邱‚ئ‚ھ‚إ‚«‚ـ‚·پB
‚و‚ء‚ؤپC‚ ‚é“d‰×Q‚©‚ç‹——£‚’‚ج“dٹE‚ًE‚ئ‚µپA‚»‚ج’n“_‚ة’Pˆت“d‰×‚P[C]‚ً’u‚¢‚½‚ئ‚«”گ¶‚·‚éƒNپ[ƒچƒ“—ح‚ًF‚ئ‚·‚é‚ئپA
پ@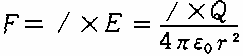
‚ن‚¦‚ة
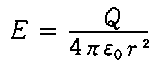
Eپ@پ@پF“dٹE‚ج‹‚³ [V/ m]
Qپ@پ@پF‚ ‚é“d‰×‚ج“d‹C—ت[C]
‚’پ@پ@پF“_“d‰×‚©‚ç“dٹE‚ج‹‚³‚ً‹پ‚ك‚é“_‚ـ‚إ‚ج‹——£[m]
ƒأoپ@پFگ^‹َ‚ج—U“d—¦[F/m]=8.855پ~10 -12
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پi“dٹE‚ج‹‚³‚ج‚ـ‚ئ‚كپj
‡@‚ب‚ة‚ھ‚µ‚©‚ج“d‹C—ح‚ھ‹y‚ش‹َٹش‚ً“dٹE‚ئ‚¢‚¤پB
‡A1[C]‚ج“d‰×‚ة1[N]‚ج—ح‚ً‚¨‚و‚ع‚·“dٹE‚ج‹‚³‚حپA1[N/C] = 1[V/m]‚إ‚ ‚éپB
‡B“dٹE‚ج‹‚³E[N/C]=E[V/m]‚ة‚¨‚¢‚ؤپAQ[C]‚ج“d‰×‚ھژَ‚¯‚éگأ“d—حپiƒNپ[ƒچƒ“—حپj‚ًF[N]‚ئ‚é‚ئپAF=QE‚ـ‚½‚ح E=F/Q‚ئ‚ب‚éپB
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
‚RپC“dˆت‚ج•â‘«گà–¾
“dٹE“à‚جٹîڈ€“_‚©‚çپC“dٹE“à‚ج‚ ‚é1“_‚ة1[CپFƒNپ[ƒچƒ“]‚جگ³“d‰×‚ًˆع“®‚³‚¹‚é‚ج‚ة•K—v‚بژdژ–V‚ً‚»‚ج“_‚ج“dˆت‚ئ‚¢‚¢‚ـ‚·پB
‚آ‚ـ‚èٹîڈ€“_‚©‚ç+1[C]‚ج“d‰×‚ًˆع“®‚³‚¹‚é‚ج‚ة1[JپFƒWƒ…پ[ƒ‹]‚جژdژ–‚ً—v‚·‚é‚و‚¤‚ب“dٹE“à‚ج1“_‚ج“dˆت‚ً1[V]‚ئ‚¢‚¢‚ـ‚·پBVپiƒ{ƒ‹ƒgپj‚ھ“dˆت‚ج’Pˆت‚إ‚·پB
ٹîڈ€“_‚©‚ç“dˆت‚ھV[V]‚ج‚ئ‚±‚ë‚ةQ[C]‚ج“d‰×‚ًˆع“®‚³‚¹‚é‚ج‚ة—v‚·‚éژdژ–‚ًW[J]‚ئ‚·‚ê‚خپCW=QV‚ئ‚ب‚è‚ـ‚·پB
2“_ٹش‚ج“dˆت‚جچ·‚ً“dˆتچ·‚ـ‚½‚ح“dˆ³‚ئ‚¢‚¢‚ـ‚·پB
(•½گ¬‚X”N“dŒ±‚Rژيپ@—ک_ڈo‘èپj
گ^‹َ’†‚ة‚¨‚©‚ꂽ•½چs“d‹ة”آٹش‚ةپA’¼—¬“dˆ³V[V]‚ً‰ء‚¦‚ؤ•½“™“dٹEE[V/m]‚ًچى‚èپA‚±‚ج‰A‹ة”آ‚ة“dژq‚ً‚¨‚¢‚½ڈêچ‡پAڈ‰‘¬“x—ë‚إڈo”‚µ‚½“dژq‚ھ—z‹ة”آ‚ة“’B‚µ‚½‚ئ‚«‚ج‘¬“x‚حپAe[m/s]‚ئ‚ب‚ء‚½پB‚±‚ج‚ئ‚«‚ج“dژq‚ج‰^“®ƒGƒlƒ‹ƒMپ[‚حپA“dژq‚ھ—z‹ة”آ‚ة“’B‚·‚é‚ـ‚إ‚ة“¾‚éƒGƒlƒ‹ƒMپ[‚ة“™‚µ‚¢‚ئچl‚¦‚ç‚êپAژں‚جژ®‚ھگ¬—§‚·‚éپB
پ@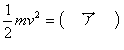 ‚½‚¾‚µپA“dژq‚ج“d‰×‚ًe[C]پA“dژq‚جژ؟—ت‚ًm[kg]‚ئ‚·‚éپB‚µ‚½‚ھ‚ء‚ؤپA‚±‚جژ®‚©‚ç“dژq‚ج‘¬“xv[m/s]‚حپA(پ@ƒCپ@)‚إ•\‚³‚ê‚éپB
‚½‚¾‚µپA“dژq‚ج“d‰×‚ًe[C]پA“dژq‚جژ؟—ت‚ًm[kg]‚ئ‚·‚éپB‚µ‚½‚ھ‚ء‚ؤپA‚±‚جژ®‚©‚ç“dژq‚ج‘¬“xv[m/s]‚حپA(پ@ƒCپ@)‚إ•\‚³‚ê‚éپB
پ@ڈم‹L‚ج‹Lڈq’†‚ج‹َ”’‰سڈٹ(ƒA)‹y‚ر(ƒC)‚ة‹L“ü‚·‚éژڑ‹ه‚ئ‚µ‚ؤپAگ³‚µ‚¢‚à‚ج‚ً‘g‚فچ‡‚ي‚¹‚½‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
| ‡@ |
eE
|
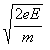
|
‡A |
eV |
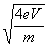 |
‡B |
|
2eV
|
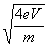
|
|
‡C |
|
eV
|
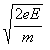
|
|
‡D |
|
eV
|
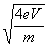
|
|
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ–â‘è‰ً“ڑ‹y‚ر‰ًگàپEپEپEپE“dژqƒ{ƒ‹ƒg‚جŒِژ®‚و‚èپA“dژq‚ج‰^“®ƒGƒlƒ‹ƒMپ[‚ح“dˆ³‚u‚ئ“dژq“d‰×‚ئ‚جگد‚ئ‚ب‚éپB‚»‚جŒِژ®‚ً‘¬“x‚–‚إ‚ئ‚‚ئ‚و‚¢پBپ@پ@گ³‰ًپ@‡C
“dژqƒ{ƒ‹ƒg‚ج•â‘«گà–¾
پu“dژqƒ{ƒ‹ƒgپv‚à‚µ‚‚حپuƒGƒŒƒNƒgƒچƒ“ƒ{ƒ‹ƒgپielectron voltپjپv‚حپA“dˆتچ·‚ج’Pˆت‚إ‚ ‚éپuƒ{ƒ‹ƒgپv‚ئ“d‰×پuƒNپ[ƒچƒ“پv‚ً‚©‚¯‚½‚à‚ج‚إپAƒGƒlƒ‹ƒMپ[‚ً•\‚µ‚ـ‚·پBƒGƒlƒ‹ƒMپ[‚إ‚·‚©‚ç’Pˆت‚حƒWƒ…پ[ƒ‹[J]‚إ‚·پD

“dژq‚جژ؟—ت‚ً‚چپA“dˆت‚ة‚و‚è“dژq‚ھ‰ء‘¬‚µ‚ؤ‘¬“x‚–‚ة‚ب‚ء‚½‚ئ‚«‚ج‰^“®ƒGƒlƒ‹ƒMپ[‚جٹضŒW‚ة‚و‚è
‚جٹضŒWژ®‚ھگ¬‚è—§‚؟‚ـ‚·پB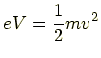 ‚±‚جƒCƒپپ[ƒWگ}‚ًژں‚ةژ¦‚µ‚ـ‚·پB
‚±‚جƒCƒپپ[ƒWگ}‚ًژں‚ةژ¦‚µ‚ـ‚·پB
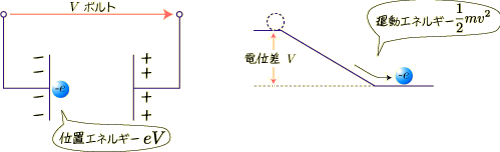
‚g‚P‚T“dŒ±‚Rژي—ک_
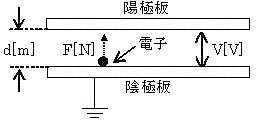
پ@گ}‚ج‚و‚¤‚ةپAگ^‹َ’†‚ة“d‹ةٹشٹud[m]‚ج•½چs”آ“d‹ة‚ھ‚ ‚èپA‰A‹ة”آڈم‚ة“dژq‚ً’u‚¢‚½پB—z‹ة”آ‚ة“dˆ³V[V]‚ً‰ء‚¦‚½‚ئ‚«پA‚±‚ج“dژq‚ة‰ء‚ي‚é—حF[N]‚جژ®‚ئ‚µ‚ؤپAگ³‚µ‚¢‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
پ@‚½‚¾‚µپA“dژq‚جژ؟—ت‚ًm[kg]پA“d‰×‚جگâ‘خ’l‚ًe[C]‚ئ‚·‚éپB‚ـ‚½پA“d‹ة”آ‚ج’[Œّ‰ت‚ح–³ژ‹‚إ‚«‚é‚à‚ج‚ئ‚·‚éپB
|
‡@
|
V2e/d
|
‡A
|
Vem/d2
|
‡B
|
Vm/(d2e)
|
‡C
|
Ve/d2
|
‡D
|
Ve/d
|
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ‰ًگà‚¨‚و‚ر‰ً“ڑ
“dٹEE‚ج’†‚إپA“d‰×e‚ھژَ‚¯‚é—ح‚حپAŒِژ®‚ة‚و‚è
FپپeEپ@(N)‚ئ‚ب‚éپB
‰A‹ة”آپ`—z‹ة”آ‚جٹشٹud[m]‚ة“dˆ³V[V]‚ً‰ء‚¦‚ؤ‚¢‚é‚ج‚إپA“dٹEE‚حVپ^d‚إ‚ ‚éپB
Œج‚ةپ@Fپپeپ~EپپeVپ^dپ@(N)
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@‰ً“ڑپ@‡D
‚g‚P‚R“dŒ±‚Rژي—ک_
پ@گأ“dٹE‚ةٹض‚·‚éژں‚ج‹Lڈq‚ج‚¤‚؟پAŒë‚ء‚ؤ‚¢‚é‚ج‚ح‚ا‚ê‚©پB
|
‡@
|
”}ژ؟’†‚ة’u‚©‚ꂽگ³“d‰×‚©‚çڈo‚é“d‹C—حگü‚ج–{گ”‚حپA‚»‚è“d‰×‚ج‘ه‚«‚³‚ة”ن—ل‚µپA”}ژ؟‚ج—U“d—¦‚ة”½”ن—ل‚·‚éپB
|
|
‡A
|
“dٹE’†‚ة‚¨‚¯‚é“d‹C—حگü‚حپA‘ٹŒف‚ةŒً‚³‚µ‚ب‚¢پB
|
|
‡B
|
“dٹE’†‚ة‚¨‚¯‚é“d‹C—حگü‚حپA“™“dˆت–ت‚ئŒًچ·‚·‚éپB
|
|
‡C
|
“dٹE’†‚ج‚ ‚é“_‚ج“d‹C—حگü‚ج–§“x‚حپA‚»‚ج“_‚ة‚¨‚¯‚é“dٹE‚ج‹‚³(‘ه‚«‚³)‚ً•\‚·پB
|
|
‡D
|
“dٹE’†‚ة’u‚©‚ꂽ“±‘ج“à•”‚ج“dٹE‚ج‹‚³(‘ه‚«‚³)‚حپA‚»‚ج“±‘ج•\–ت‚ج“dٹE‚ج‹‚³(‘ه‚«‚³)‚ة“™‚µ‚¢پB
|
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ‰ًگà‚¨‚و‚ر‰ً“ڑ
‡@“d‹C—حگü‚m‚ئ“d‰×‚p‚ئ—U“d—¦ƒأ‚جٹضŒW‚حپA
‚mپپ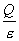 ‚إ‚ ‚éپB
‚إ‚ ‚éپB
‚آ‚ـ‚èپA“d‹C—حگü‚حپA“d‰×‚ة”ن—ل‚µپA—U“d—¦‚ة”½”ن—ل‚·‚éپB
‡A“d‹C—حگü‚حگ³“d‰×‚©‚çڈo‚ؤپA•‰“d‰×‚إڈI‚ي‚èپA“d‹C—حگü“¯ژmŒًچ·‚µ‚ب‚¢پB
‡B“d‹C—حگü‚جگعگü•ûŒü‚ھ“dٹE‚ج•ûŒü‚إ‚ ‚èپA“™“dˆت–ت‚ئŒًچ·‚·‚éپB
‡C’f–تگد‚P‡u“–‚½‚è‚ج“d‹C—حگü‚ج–§“x‚ھ“dٹE‚ج‹‚³‚إ‚ ‚éپB
‡D“±‘ج“à•”‚ج“dٹE‚ج‹‚³‚حƒ[ƒچ‚إ‚ ‚éپB‚»‚ج‚½‚ك“±‘ج•\–ت‚ج“dٹE‚ج‹‚³(‚ة“™‚µ‚¢‚حٹشˆل‚¢‚إ‚ ‚éپBپ@
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@‰ً“ڑپ@‡D
H12“dŒ±‚Rژي—ک_
پ@‹َ‹C’†‚ةŒا—§‚µ‚½”¼Œaa[m]‚ج“±‘ج‹…‚ة‘ر“d‚إ‚«‚éچإ‘ه‚ج“d‰×[C]‚ج’l‚ئ‚µ‚ؤپAگ³‚µ‚¢‚à‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
پ@‚½‚¾‚µپA‹َ‹C‚جگâ‰ڈ‘د—ح‹y‚ر—U“d—¦‚ح‚»‚ꂼ‚êEm[V/m]‹y‚رƒأo[F/m]‚ئ‚·‚éپB
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ‰ًگà‚¨‚و‚ر‰ً“ڑ
‹َ‹C’†‚ة•‚‚©‚ٌ‚¾”¼Œaa(m)‚ج“±‘ج‹…‚ج“d‰×‚ًQ‚ئ‚·‚é‚ئ‹…•\–ت‚ج“dٹE‹“xE‚حپAŒِژ®‚ة‚و‚èپ@پ@پ@پ@پ@پ@پ@
Eپپ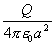
‚±‚ج“dٹE‹“xE‚ھ‹َ‹C‚جگâ‰ڈ‘ج—ح‚ئ“™‚µ‚¢‚ئ‚«‚ھ‘ر“d‚إ‚«‚éچإ‘ه“d‰×‚ئ‚ب‚éپB
ڈمژ®‚جE‚ھEm‚ج‚ئ‚«‚جQ‚ً‹پ‚ك‚é‚ئ
Q=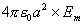
پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@پ@‰ً“ڑپ@‡C
H15“dŒ±‚Rژي—ک_
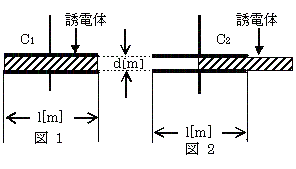
پ@گ^‹َ’†‚ة‚¨‚¢‚ؤپAˆê•س‚Œ[m]‚جگ³•ûŒ`“d‹ة‚ًٹشٹud[m]‚إ”z’u‚µ‚½•½چs”آƒRƒ“ƒfƒ“ƒT‚ھ‚ ‚éپBگ}1‚ح‚±‚جƒRƒ“ƒfƒ“ƒT‚ج“d‹ة”آٹش‚ة”ن—U“d—¦ƒأr=3‚ج—U“d‘ج‚ً‘}“ü‚µ‚½ڈَ‘شپAگ}2‚حگ}1‚ج—U“d‘ج‚ً“d‹ة–تگد‚ج1/2‚¾‚¯ˆّ‚«ڈo‚µ‚½ڈَ‘ش‚ًژ¦‚µ‚ؤ‚¢‚éپBگ}1‹y‚رگ}2‚ج“ٌ‚آ‚جƒRƒ“ƒfƒ“ƒT‚جگأ“d—e—تC1[F]‹y‚رC2[F]‚ج”ن(C1:C2)‚ئ‚µ‚ؤپAگ³‚µ‚¢‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
پ@‚½‚¾‚µپAl>>d‚إ‚ ‚èپAƒRƒ“ƒfƒ“ƒT‚ج’[Œّ‰ت‚ح–³ژ‹‚إ‚«‚é‚à‚ج‚ئ‚·‚éپB
|
‡@
|
پ@2:1
|
‡A
|
پ@3:1
|
‡B
|
پ@3:2
|
‡C
|
پ@4:3
|
‡D
|
پ@5:4
|
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ‰ًگà‚¨‚و‚ر‰ً“ڑ
ƒRƒ“ƒfƒ“ƒT‚ج—e—ت‚حپA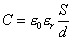 ‚إ•\‚·‚±‚ئ‚ھ‚إ‚«‚éپBپ@
‚إ•\‚·‚±‚ئ‚ھ‚إ‚«‚éپBپ@
 ‚حپAگ^‹َ‚ج—U“d—¦پA
‚حپAگ^‹َ‚ج—U“d—¦پA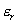 ‚حپA”}‘ج‚ج”ن—U“d—¦,
‚حپA”}‘ج‚ج”ن—U“d—¦,
S‚حپA“d‹ة‚ج–تگد,‚„‚حپA“d‹ةٹش‚ج‹——£
گ}‚P‚جƒRƒ“ƒfƒ“ƒT—e—تC1‚حپA
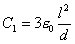
گ}2‚جƒRƒ“ƒfƒ“ƒT—e—تC2‚حپA“d‹ة–تگد‚ھC‚P‚ج‚P/‚Q‚إ‚ ‚éگ^‹َ—U“d—¦‚جƒRƒ“ƒfƒ“ƒT‚ئپA“d‹ة–تگد‚ھC‚P‚ج‚P/‚Q‚إ‚ ‚é”ن—U“d—¦‚ھ‚R‚جƒRƒ“ƒfƒ“ƒT‚ھ•ہ—ٌ‚ةگع‘±‚³‚ꂽڈَ‘ش‚ئ“¯‚¶‚إ‚ ‚éپB‚ن‚¦‚ةC2‚حپA
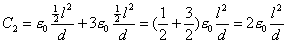
‚ن‚¦‚ةپ@C1پFC2پپ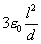 پF
پF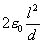 پپ3پF‚Q
پپ3پF‚Q
‰ً“ڑپ@‡B
پiH10“dŒ±‚Rژي—ک_پj
پ@“dˆ³V[V]‚ةڈ[“d‚³‚ꂽگأ“d—e—تC[F]‚جƒRƒ“ƒfƒ“ƒT‚ئ‘S‚ڈ[“d‚³‚ê‚ؤ‚¢‚ب‚¢گأ“d—e—ت0.5C[F]‚جƒRƒ“ƒfƒ“ƒT‚ئ‚ھ‚ ‚éپB‚±‚ê‚ç“ٌ‚آ‚جƒRƒ“ƒfƒ“ƒT‚ً•ہ—ٌ‚ةگع‘±‚µ‚½‚ئ‚«پA‚±‚ê‚ç‚جƒRƒ“ƒfƒ“ƒT‚ة’~‚¦‚ç‚ê‚é‘Sگأ“dƒGƒlƒ‹ƒMپ[[J]‚ج’l‚ئ‚µ‚ؤگ³‚µ‚¢‚à‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ‰ًگà‚¨‚و‚ر‰ً“ڑ
“dˆ³V‚إڈ[“d‚³‚ꂽƒRƒ“ƒfƒ“ƒTC‚ج“d‰×‚ًQ‚ئ‚·‚é‚ئپAQ=CV‚إ‚ ‚éپB
‚Q‚آ‚جƒRƒ“ƒfƒ“ƒT‚ً•ہ—ٌگع‘±‚·‚é‚ج‚إپAچ‡گ¬گأ“d—e—ت‚ًC2‚ئ‚·‚é‚ئپA
C2پپC+0.5Cپپ1.5C
ƒRƒ“ƒfƒ“ƒT‚ة’~‚¦‚ç‚ê‚éگأ“dƒGƒlƒ‹ƒMپ[‚حژںژ®‚إ‚ ‚éپB
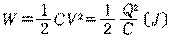 پ@
پ@
•ہ—ٌگع‘±Œم‚ج‘چ“d‰×—ت‚ة•د‰»‚ھ‚ب‚¢‚ج‚إپA‘S“d‰×‚حCV‚إ‚ ‚èپAگأ“d—e—ت‚ح1.5C‚إ‚ ‚éپB•ہ—ٌگع‘±Œم‚جگأ“dƒGƒlƒ‹ƒMپ[‚ًW2‚ئ‚·‚é‚ئپA
W2پپ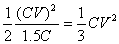 پ@پiJپjپ@پ@‰ً“ڑ‡C
پ@پiJپjپ@پ@‰ً“ڑ‡C
پiH‚X“dŒ±‚Rژي—ک_پj
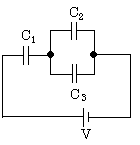
گأ“d—e—ت‚ھ‚»‚ꂼ‚êC1[F]پAC2[F]‹y‚رC3[F]‚ج3Œآ‚جƒRƒ“ƒfƒ“ƒT‚ًگ}‚ج‚و‚¤‚ةگع‘±‚µپA’¼—¬“dˆ³V[V]‚ً‰ء‚¦‚½‚ئ‚«پAƒRƒ“ƒfƒ“ƒTC2‚ة’~‚¦‚ç‚ê‚é“d‰×‚ج’l[C]‚ئ‚µ‚ؤپAگ³‚µ‚¢‚à‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ‰ًگà‚¨‚و‚ر‰ً“ڑ
•ہ—ٌƒRƒ“ƒfƒ“ƒTC2‚ئC3‚جچ‡گ¬گأ“d—e—ت‚ًC23‚ئ‚·‚é‚ئپA
C23پپC2پ{C3
C1‚ئC23‚ح’¼—ٌ‚ب‚ج‚إپAC23‚ة‰ء‚ي‚é“dˆ³‚ًV23‚ئ‚·‚é‚ئپA
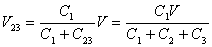
ƒRƒ“ƒfƒ“ƒTC2‚ة’~‚¦‚ç‚ê‚é“d‰×‚ج’l‚ًQ2‚ئ‚·‚é‚ئپA
Q2پپC2پ~V23پپ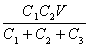 پ@پ@پ@‰ً“ڑپ@‡D
پ@پ@پ@‰ً“ڑپ@‡D
پiH‚X“dŒ±‚Rژي—ک_پj
گ}‚ج‰ٌکH‚ة‚¨‚¢‚ؤپAƒXƒCƒbƒ`S‚ھٹJ‚¢‚ؤ‚¢‚é‚ئ‚«پAگأ“d—e—تC1=0.004[F]‚جƒRƒ“ƒfƒ“ƒT‚ة‚ح“d‰×Q1=0.3[C]‚ھ’~گد‚³‚ê‚ؤ‚¨‚èپAگأ“d—e—تC2=0.002[F]‚جƒRƒ“ƒfƒ“ƒT‚ج“d‰×‚حQ2=0[C]‚إ‚ ‚éپB‚±‚جڈَ‘ش‚إƒXƒCƒbƒ`‚r‚ً•آ‚¶‚ؤپA‚»‚ê‚©‚çژٹش‚ھڈ\•ھ‚ةŒo‰ك‚µ‚ؤ‰ك“nŒ»ڈغ‚ھڈI—¹‚µ‚½پB‚±‚جٹش‚ة’ïچRR[ƒ¶]‚إڈء”‚ꂽ“d‹CƒGƒlƒ‹ƒMپ[[J]‚ج’l‚ئ‚µ‚ؤپAگ³‚µ‚¢‚ج‚حژں‚ج‚¤‚؟‚ا‚ê‚©پB
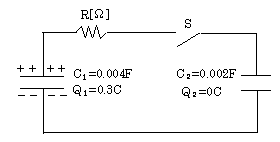
‡@2.50پ@‡A3.75پ@‡B7.50پ@‡C11.25پ@‡D13.33
پEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپEپE
پڑ‰ًگà‚¨‚و‚ر‰ً“ڑ
ƒRƒ“ƒfƒ“ƒT‚ة’~‚¦‚ç‚ê‚éگأ“dƒGƒlƒ‹ƒMپ[‚حژںژ®‚إ‚ ‚éپB
پ@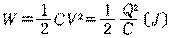
C‚P‚جگأ“dƒGƒlƒ‹ƒMپ[‚ًW‚P‚ئ‚·‚é‚ئپA
W1پپ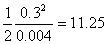 پ@پiJپj
پ@پiJپj
ƒXƒCƒbƒ`S‚ً•آ‚¶‚½‚ئ‚«‚جچ‡گ¬گأ“d—e—ت‚ًC2‚ئ‚·‚é‚ئ
C2پپ0.004پ{0.002پپ0.006پ@پiFپj
ƒXƒCƒbƒ`S‚ً•آ‚¶‚½‚ئ‚«‚ج‘S“d‰×‚ح0.3پiCپj‚ب‚ج‚إپA‚±‚ج‚ئ‚«‚جگأ“dƒGƒlƒ‹ƒMپ[‚ًW2‚ئ‚·‚é‚ئ
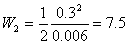 پ@پiJپj
پ@پiJپj
‚ن‚¦‚ةپAR‚إڈء”‚ê‚éƒGƒlƒ‹ƒMپ[‚ح
W1پ|W2پپ11.25پ|7.5پپ3.75پ@پiJپjپ@پ@‰ً“ڑ‡A
| ”شچ† |
چ€پ@–ع |
Œِپ@ژ® |
| ‚P |
“d‰×‚ةٹض‚·‚éƒNپ[ƒچƒ“‚ج–@‘¥پiگ^‹َ’†پj |
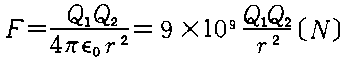 |
| ‚Q |
“dٹE‚ج‹‚³پiگ^‹َ’†پj |
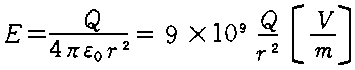 |
| ‚R |
“_“d‰×‚ة‚و‚é“dˆت
پiگ^‹َ’†پj |
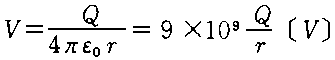 |
| ‚S |
“dژqƒ{ƒ‹ƒg |
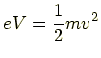 |
| ‚T |
“d‘©–§“x |
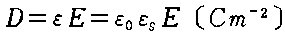 |
| ‚U |
گأ“d—e—تپiˆê”تپj |
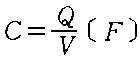 |
| ‚V |
گأ“d—e—تپi•½چs”آٹشپj |
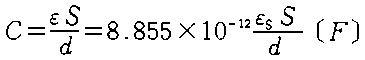 |
‚W
|
گأ“dٹE‚ة’~گد‚³‚ê‚é
ƒGƒlƒ‹ƒMپ[–§“x |
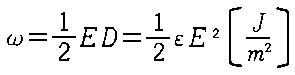 |
‚X
|
گأ“d—e—ت‚ة’~گد‚³‚ê‚é
ƒGƒlƒ‹ƒMپ[ |
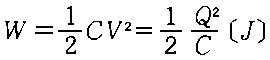 |

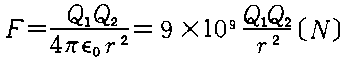

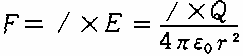
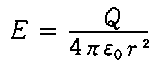
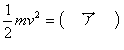
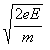
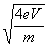
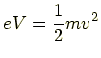 ‚±‚جƒCƒپپ[ƒWگ}‚ًژں‚ةژ¦‚µ‚ـ‚·پB
‚±‚جƒCƒپپ[ƒWگ}‚ًژں‚ةژ¦‚µ‚ـ‚·پB