（H15 電験３種理論）
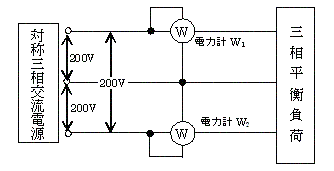
図のように、線間電圧200[V]の対称三相交流電流電源から三相平衡負荷に供給する電力を二電力計法で測定する。2台の電力計W1及びW2を正しく接続したところ、電力計W2の指示が逆振れを起こした。
電力計W2の電圧端子の極性を反転して接続した後、2台の電力計の指示値は、電力計W1が490[W]、電力計W2が25[W]であった。
このときの対称三相電源が三相平衡負荷に供給する電力[W]の値として、正しいのはどれか。
ただし、三相交流電源の相回転は、a、b、cの順とし、電力計の電力損失は無視できるものとする。
① 25 ② 258 ③ 465 ④ 490 ⑤ 515
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
ブロンデルの定理により、ｎ相の電力は、(n－1)個の電力計で測定できる。３相の場合は２個の電力計で測定できる。これを２電力計法という。この方法での電力測定は、２つの計器の読みW1とW2の和となる。しかし、負荷の力率が50％すなわち力率角が60度のとき１方の計器の読みがセロ（W2＝０）となる。これ以下の力率では読みが逆振れするので、電力コイルの接続を切り替える。このときの電力は、計器の読みの差（W1－W2）となる。
題意より電力は、490－25＝465 (W) 解答 ③
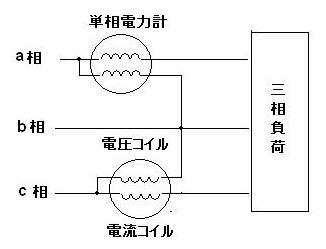
図 ２電力計法による三相3線結線
（H13 電験３種理論）
図は、単相交流6,600[V]の電源に接続されている負荷の電力及び力率を発信装置付電力計及び電流計を用いて計測する回路である。この場合、次の(a)及び(b)に答えよ。
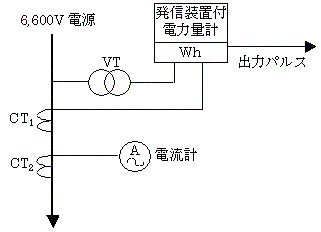
(a) 計器用変圧器VT及びCT1の二次側に接続した電力量計の発信装置の出力パルスを、負荷が安定している10分間測定したところ、そのパルス数は130であった。この負荷の1時間当たりの消費電力量[kWh]の値として、正しいのは次のうちどれか。
ただし、この電力量計の発信装置の1[kWh]当たりの出力パルス数は4,000である。また、VT及びCT1の一次定格/二次定格は、それぞれ6,600V/110V及び100/5Aである。
① 202 ② 234 ③ 245 ④ 278 ⑤ 300
(b) この負荷に流れる電流を変流器CT2の二次側に接続した電流計で測ったところ、電流計は2.0[A]を示した。この負荷の力率[%]の値として正しいのは次のうちどれか。
ただし、変流器CT2の一次側定格/二次側定格は、100/5Aである。
① 76 ② 82 ③ 85 ④ 89 ⑤ 92
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
(a) 10分間のパルス数が130なので、この負荷の1時間当たりのパルス数は、
130×(60/10)＝780 （パルス） 故に２次側電力量は780/4000 （KWｈ）となる。
また、VT及びCT1の一次定格/二次定格（変換率）が、それぞれ6,600V/110V＝60 及び100/5A＝20なので、１次側の電力量は２次側電力量の60×20倍となる。
故に１次側電力量は、(780/4000)×60×20＝234 （KWｈ） 解答 ②
(b) 変流器CT2の一次側定格/二次側定格（変換率）が100/5Aであり、電流計は2.0[A]を示しているので、１次側の電流は２×20＝40(A)である。
単相電力をWとし、電圧をV、電流をI、力率をcosθとすると、W=VIcosθとなる。
ゆえに、234000=6600×40×cosθ
これをcosθで解くとcosθ＝0.889 ゆえに力率は 約89％ 解答 ④
(H15 電験３種理論）
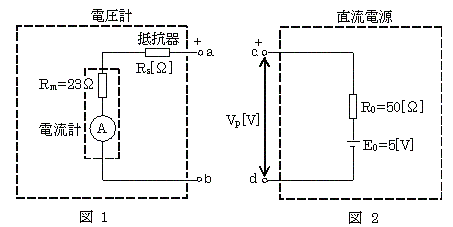
図1のように、定格電流1[mA]、内部抵抗Rm=23[Ω]の電流計と抵抗Rs[Ω]の抵抗で構成された定格電圧5[V]の電圧計がある。
次の(a)及び(b)に答よ。
ただし、電圧計として用いる電流計の目盛り0～1[mA]は、0～5[V]に読み替えるものとし、電圧計の端子aは正極とする。
(a) この抵抗器のRs[Ω]の値として、正しいものは次のうちどれか。
① 4.947 ② 4.960 ③ 4.977 ④ 5.000 ⑤ 5.023
(b) 図2のような電圧E0[Rs[V]、内部抵抗Rm=50[Ω]の直流電源の端子c、dに、この電圧計の端子a、bをそれぞれ接続し、電圧Vp[V]を測定した。電圧計が指示したVp[V]の値として、最も近いのは次のうちどれか。
① 4.90 ② 4.95 ③ 4.97 ④ 5.00 ⑤ 6.02
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
(a)図１において、端子ab間に5Vを加えたときの電流が1[mA]なので次式が成立する。
これを解くと Rs＝5000－23＝4977 (Ω) 解答 ③
(b)図１・図２において、端子a－c、と端子b－dをそれぞれ接続すると、電圧計の5000Ωと電源側の50Ωと電源5Vの直列回路になる。ゆえに電圧計が指示Vp[V]の値は、
(V) 解答 ②
（H11 電験３種理論）
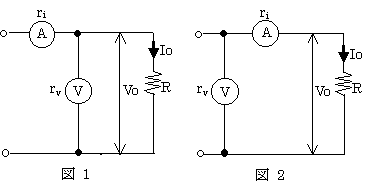
電圧計V及び電流計Aを用いて負荷抵抗R[Ω]で消費される直流電力を測定するとき、計器の接続を図1又は図2とした場合のそれぞれの測定値の誤差ε1及びε2を表す式として、正しいものの組み合わせは次のうちどれか。ただし、電圧計の内部抵抗をrv[Ω]、電流計の内部抵抗をri[Ω]、負荷電圧をVo[V]、負荷電流をIo[A]とする。
|
① |
|
② |
|
③ |
|
|
④ |
|
⑤ |
|
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
☆測定値の誤差は、(測定値)－(真値)となる。題意における真値の電力はV0I0となる。
図１において、電流計Aの測定値は、I0＋V0/rVとなる。そのため測定電力はV0(I0＋V0/rV）
となり、誤差ε1は、ε1＝V0(I0＋V0/rV)－V0I0＝V0・V0/rV＝I0R・V0/rV＝R/rV ・I0V0
☆図２において、電圧計Vの測定値は、I0・ｒi＋V0となる。そのため測定電力はI0(I0・ｒi＋V0）
となり、誤差ε2は、ε2＝I0(I0・ｒi＋V0）－V0I0＝I0・I0・ｒi＝V0/R・I0・ｒi＝ｒi/R・I0V0
解答 ④
（H12 電験３種理論）
表は、正弦波交流電圧v[V]を全波整流及び半波整流した場合の整流波形について、それぞれの平均値[V]及び実効値[V]を示したものである。表中の空白箇所( ア )及び( イ )に記入する式として、正しいものを組み合わせたのは次のうちどれか。
|
|
|
|||||||||||||||||||
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
（ア）正弦波の実効値は最大値を
で割ったもの、つまり
となる。
（イ）正弦波の半波整流値の平均値（面積）は全波整流波の1/2なので、
÷2により
となる。
解答 ④
●実効値
交流電圧は実効値で呼ぶことが一般です。この実効値は、時間的に変化する交流をエネルギー（電力）を直流エネルギーに換算したものといえます。数学的に言えば「２乗の平均の平方根(ルート)」であり、「Root Mean of Square value」を略してRMS(アール・エム・エス)と言います。
そのため、交流電圧の実効値Vは、 V=
これを計算するとV=＝
となる。
これを図示すると下図のようになる。
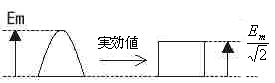
●平均値
交流電圧の平均値を式で表すと 
となる。これは時間的に変化する交流面積を直流面積に変換したものであり、これを計算するとV=
となる。
これを図示すると下図のようになる。
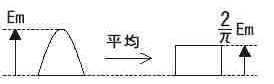
●波形率
波形率とは、実効値／平均値である。
●波高値
波高値とは、最大値／実効値である。
（参考までに）
|
名称 |
最大値 |
実効値 |
平均値 |
波形率 |
波高値 |
|
正弦波 |
Ｅｍ |
Ｅｍ／√2 |
Ｅｍ・2／π |
π／2√2 |
√2 |
|
半波整流波 |
Ｅｍ |
Ｅｍ／２ |
Ｅｍ／π |
π／2 |
２ |
|
全波整流波 |
Ｅｍ |
Ｅｍ／√2 |
Ｅｍ・2／π |
π／2√2 |
√2 |
（H11 電験３種理論）
内部抵抗3[kΩ]、最大目盛1[V]の電圧計を利用して最大100[V]まで測定できるようにするために必要な倍率器の抵抗[kΩ]として、正しい値は次のうちどれか。
[ ① 290 ② 297 ③ 300 ④ 303 ⑤ 330 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
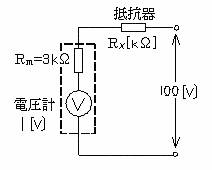
倍率器の抵抗をRx（kΩ）とすると、100（V）を加えたときに電圧計に流れる電流Iは、
I＝100÷（Rx＋３） （mA）
内部抵抗3[kΩ]、最大目盛1[V]の電圧計なので、この電流の最大値は、１÷３ （mA）である。
題意より上記２つの電流が等しいので、
100÷（Rx＋３）＝１÷３ Rx＋３＝300 ゆえに Rx＝297 （kΩ） 解答 ②
（H10 電験３種理論）
指示電気計器の動作原理について次の記述のうち、誤っているのはどれか。
|
① |
整流形:ダイオードなどの整流素子を用いて交流を直流に変換し、可動コイル形計器で指示させる方式 |
|
② |
熱電形:発熱線に流れる電流によって熱せられる熱電対に生じる起電力を、可動コイル形計器で指示させる方式 |
|
③ |
可動コイル形:固定コイルに流れる電流の磁界と、可動コイルに流れる電流との間に生じる力によって可動コイルを駆動させる方式 |
|
④ |
静電形:異なる電位を与えられた固定電極と可動電極との間に生じる起電力によって、可動電極を駆動させる方式 |
|
⑤ |
可動鉄片形:固定コイルに流れる電流の磁界と、その磁界によって磁化された可動鉄片との間に生じる力により、又は固定コイルに流れる電流によって固定鉄片及び可動鉄片を磁化し、両鉄片間に生じる力により可動鉄片を駆動させる方式 |
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
(3)の可動コイル形計器は、永久磁石で作られる磁界と可動コイルに流れる電流によって発生する電磁力（フレミングの左手の法則）を利用した計測器である。そのため固定子にコイルはない。
解答 ③
