1�A���C�O�a�@
2�A������
3�A���C���[�����g�@
4�A���C�̃q�X�e���V�X
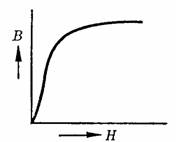
�S�Ȃǂ̋������̂���������ƁA������H�������Ƃ��̎������xB�̊W�͐}1�̂悤�ɂȂ�܂��B�}�ŕ�����悤�Ɏ����͂������ɂ��B�̑����������݂��Ă��܂��B����͎����̂̒��Ŏ������ߖ��������ċN���錻�ۂŁA���̂悤�Ȍ��ۂ����C�O�a�Ƃ����܂��B����H��B�̊W��\��}�̂悤�ȋȐ������C�O�a�Ȑ��Ƃ����܂��B
�������̎�����H�̂Ƃ�,B�̎������x�����Ƃ�,B�^H�����Ƃ����܂��B���̓������́A�P�ʒ�,�P�ʒf�ʐςɂ����鎥�C��R�̋t���Ƃ��Ă���`����Ă��܂��B
B=��H�̊W�����o���Ă����A��= B�^H���o�܂��B
�k���l������(��)=�^��̓�����(��o)�~�䓧����(��s)
���ɂ̋������Ƃ��A���ɖ�̋��������Ƃ���ƁA���~�������̎��C���[�����g�Ƃ����܂��B
��Ԏ����͂��������̂̎������xB��,���̎�����H�̕ω��̌o���ɊW��,�}�̂悤�ȃq�X�e���V�X���[�v(��)��`���܂��B���̌��ۂ����C�̃q�X�e���V�X�Ƃ����܂��B�q�X�e���V�X���[�v�ň͂܂ꂽ�ʐςɔ�Ⴕ�������i�q�X�e���V�X���j���܂��B
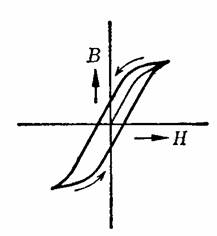
�iH12�d���R����j
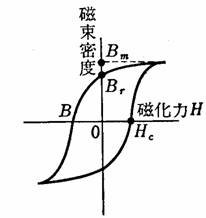
�@�}�͋������̂̃q�X�e���V�X���[�v�������B�}����Br�y��Hc�́A���ꂼ��(�@�A�@)�y��(�@�C�@)�̑傫����\���B��ʂɁABr���傫����Hc�̏����������̂�(�@�E�@)�ɓK���ABr���傫�����AHc���傫���������̂́A(�@�G�@)�ɓK����B
��L�̋L�q���̋ӏ�(�@�A�@)�A(�@�C�@)�A(�@�E�@)�y��(�@�G�@)�̋L��������Ƃ��āA���������̂�g�ݍ��킹���͎̂��̂����ǂꂩ�B
|
�@�@ |
(�A)�ێ��� |
(�C)������ |
(�E)�d���� |
(�G)�i�v���@ |
|
�@�A |
(�A)�c�����C |
(�C)�ێ��� |
(�E)�d���� |
(�G)�i�v���@ |
|
�@�B |
(�A)�ێ��� |
(�C)�c������ |
(�E)�i�v���� |
(�G)�d���@ |
|
�@�C |
(�A)�c�����C |
(�C)�ێ��� |
(�E)�i�v���� |
(�G)�d���@ |
|
�@�D |
(�A)���ώ������x |
(�C)������ |
(�E)�d���� |
(�G)�i�v���@ |
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i����y�щj
�}�ɂ����āABm�͍ő厥�����x�ABr�͎c�����C�AHc�͕ێ��͂Ƃ����܂��B�i�v���ɒ~�����鎥�C�G�l���M�[�́A�ar�gc�^�Q�ł���A���ꂪ�傫���قlji�v���ɓK���Ă���B����d���Ƃ��ẮA�q�X�e���V�X���������������悢�B�iH�����������j�܂��ABr���傫����Hc���������������̂́A�����ȗ㎥�d���ő傫�Ȏ��C�������ƂɂȂ�̂ŁA�d���ɓK���Ă���B�@�@�@�@�@�@�@�@�@�@�@�@�A
�iH10�d�C���_����j
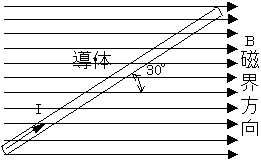
�}�̂悤�Ɏ������xB=0.5[T]�̈�l�Ȏ��E�̒��ɒ�����̓��̂����E�̕����ɑ���30���̊p�x�ɂ����A�����I=100[A]�̒����d���𗬂����B���̂Ƃ��A���̂̒P�ʒ���������ɓ�����F[N/m]�̒l�Ƃ��āA�������͎̂��̂����ǂꂩ�B
[�@�@ �@10�@�@�A �@25�@�@�B �@38�@�@�C�@ 46�@�@�D�@ 53�@ ]
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i�y�щ���j
�P�ʒ�������Ƃ́A�����P��������Ƃ������Ƃł��B��ӂ�蓱�̂P���Ǝ������xB�Ƃ̊p�x���R�O�x�Ȃ̂ŁAB�ɑ���L���ȓ��̒����͂P�~sin30���i���j�ƂȂ�܂��B���̂ɗ����d����I�A�������xB�Ȃ��߁A���̂����F�́AF=B�~I�~�P�~sin30���ƂȂ�܂��B�䂦��F=0.5�~100�~�P�~sin30��=0.5�~100�~�P�~0.5=25[N]
���̂����E�����͂̌����AF=BIlsin30��[N]���g���Ηe�Ղɓ��������܂�B�@�@�@�@�A
�iH�P�T�@�d���R�헝�_�j
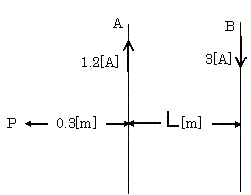
�@�}�̂悤�ɁAA�AB�Q�{�̕��s�Ȓ������̂�����A����A�ɂ�1.2[A]�A����B�ɂ͂���Ɣ��Ε�����3[A]�̓d��������Ă���B����A��B�̊Ԋu��L[m]�̂Ƃ��A����A���0.3[m]���ꂽ�_P�ɂ����鍇�����E����ɂȂ����BL[m]�̒l�Ƃ��āA�������͎̂��̂����ǂꂩ�B
�@�������A����A�AB�͖������Ƃ��A�_P�͓���A�AB���܂ޕ��ʏ�ɂ�����̂Ƃ���B
|
�@ |
0.24 |
�A |
0.45 |
�B |
0.54 |
�C |
0.75 |
�D |
1.05 |
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i����y�щj
�������̒����d���̍�锼�a���̉~����̎��E����H�́AH��![]() �ł���B
�ł���B
����A�AB�̓d���̌����͔��Ȃ̂ŁA�_P�ł݂͌��ɑł��������E�̕����ƂȂ��ӂ�荇�����E����ł���̂Ŏ��������藧�B
![]() �|
�|![]() ���O
���O
��L��L�ɂ��ĉ����Ɓ@L��0.45�@�@�@�A
�iH13�d���R��d�C���_�j
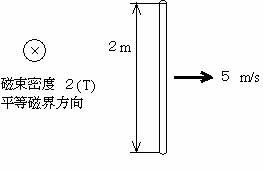
�@�������x2[T]�̕������E����l�Ɏ��ʂ̏ォ�牺�����ɉ�����Ă���A����2[m]�̒������̂����E�̕����ƒ��p�ɒu����Ă���B���̓��̂�}�̂悤��5[m/s]�̑��x�Ŏ��ʂƕ��s�Ɉړ��������Ƃ��A���̂ɔ�������U���N�d��[V]�̑傫���Ƃ��āA�������͎̂��̂����ǂꂩ�B
|
�@ |
5 |
�A |
10 |
�B |
16 |
�C |
20 |
�D |
50 |
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i����y�щ��j
�U���N�d�͂̌����ɂ��Ae�����~B�~L�@
���͑��x�im/s�j
B�͎������x(T)
L�͓��̒���(m)
�䂦��e���T�~�Q�~�Q���Q�O�iV�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�C
�iH10�d���R��d�C���_�j
�@���C��H�ɂ����鎥�C��R�Ɋւ���L�q�̂����A����Ă���̂͂ǂꂩ�B
|
�@ |
���C��R�́A���̎��ŕ\�����B
|
|
�A |
���C��R�́A���H�̒f�ʐςɔ�Ⴗ��B |
|
�B |
���C��R�́A�䓧�����ɔ���Ⴗ��B |
|
�C |
���C��R�́A���H�̒����ɔ�Ⴗ��B |
|
�D |
���C��R�̒P�ʂ́A[H-1]�ł���B |
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i��������y�щj
(1)�͓d�C�̃I�[���̖@���u���h�q�Ɠ����悤�Ɏ��C�̃I�[���̖@��������B���C�̃I�[���̖@���ł͋N���́������~���C��R�ŕ\�����Ƃ��o����B���̂��߇@�͐����B
(2)���C��R�͓d�C��R�Ɠ��l�ɍl���邱�Ƃ��o����B���C��R�͔䓧�����Ǝ��H�̒f�ʐςɔ���Ⴕ�A���H�̒����ɔ�Ⴗ��B���C��R�͒f�ʐςɔ���Ⴗ�邪�����B
(3)�䓧�����Ƃ́A���镨���̐^��̓������ɑ��銄���������Ă���B��L(2)�ŏq�ׂ��悤�ɁA���C��R�͔䓧�����ɔ���Ⴗ��B
(4)���C��R�̑傫���́A(2)�ŏq�ׂ��悤�Ɏ��H�̒����ɔ�Ⴗ��B
(5)��ӂ̒ʂ�ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�A
�@H12�d���R�헝�_
�@�^�ɂ����ꂽ����N�̉~�`�R�C���ɒ����d��I[A]�𗬂����Ƃ��A�~�`�R�C���̒��S�ɔ������鎥���̎������x[T]��\�����Ƃ��āA�������͎̂��̂����ǂꂩ�B�������A�~�`�R�C���̔��a��a[m]�A�^��̓���������0[H/m]�Ƃ���B
|
�@ |
|
�A |
|
�B |
|
�C |
|
�D |
|
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i��������y�щj
�@�������x��B[T]�A����������0[H/m]�Ƃ���ƁAB=��0H�ƂȂ�B�܂��A���aa[m]�̊���N�̉~�`�R�C���ɓd��I[A]�𗬂����Ƃ��̒��S�̎��E�̋����́A�����ɂ��H=NI/(2a) [A/m]�ł���B
��B����0H =��0 �~NI/(2a)
�@�@�@�@�@�@�@�@�@�@�@�@�@�D
H9�d���R��d�C���_
�@����30�̃R�C�����ђʂ��Ă��鎥����0.1�b�Ԃ�1[Wb]�̊����ŕω�����Ƃ��A�R�C���ɔ�������N�d��[V]�̑傫���͂����炩�B�������l�����̂�������I�ׁB
[�@�@ �@250�@�@�A �@300�@�@�B �@350�@�@�C�@ 400�@�@�D�@ 450�@ ]
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i��������y�щj
�U���N�d�͂����Ƃ���ƌ����ɂ��
e���|N![]() �@�i�}�C�i�X�͕ω���W��������̈Ӗ��j
�@�i�}�C�i�X�͕ω���W��������̈Ӗ��j
�䂦�ɁA�@e���R�O�~�P�^0.1���R�O�O�@�iV�j�@�@�@�@�A
H15�d���R��d�C���_
�@�}�̂悤�ɁA��S�S�ɃR�C��1�y�уR�C��2��������Ă���B�R�C��1�A�R�C��2�̎��ȃC���_�N�^���X�����ꂼ��L1�AL2�Ƃ��A���̊��������ꂼ��N1=100�AN2=1,000�Ƃ����Ƃ��AL1=1�~10-3[H]�ł������A���̂Ƃ��A���ȃC���_�N�^���XL2[H]�̒l�ƁA�R�C��1�ƃR�C��2�̑��݃C���_�N�^���XM[H]�̒l�Ƃ��āA���������̂�g�ݍ��킹�Ă��͎̂��̂����ǂꂩ�B
�@�������A�S�S�͓��f�ʁA�����ł���A�R�C���y�ѓS�S�̘R�ꎥ���͂Ȃ����̂Ƃ���B

|
�@ |
L2[H] |
M�@[H] |
|
�@ |
1�~10-1 |
1�~10-2 |
|
�A |
1�~10-1 |
1�~10-3 |
|
�B |
1�~10-2 |
1�~10-2 |
|
�C |
1�~10-2 |
1�~10-3 |
|
�D |
1�~10-4 |
1�~10-4 |
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
���i��������y�щj
�@L2�����߂�
�k1![]() ��N1
��N1![]() �@����ɂ��@��1��L1
�@����ɂ��@��1��L1![]()
L2![]() ��N2
��N2![]() �@�@����ɂ���@��2��L2
�@�@����ɂ���@��2��L2![]() �@
�@
��ӂ��R�ꎥ�����������߃�1����2�ƂȂ�B
�䂦��
�@L1![]() ��L2
��L2![]()
�䂦��
L2��L1�~![]() �~
�~![]()
![]() ��102�@�@�@�܂��A�R�C���ɗ����d���͊�����ɔ���Ⴗ��̂�
��102�@�@�@�܂��A�R�C���ɗ����d���͊�����ɔ���Ⴗ��̂�![]() ��
��![]() �ƂȂ�B
�ƂȂ�B
�̂�L2��L1�~![]() ���P�~
���P�~![]() �~
�~![]() ��
��![]() �i�g�j
�i�g�j
�AM�����߂�
�R�C���̑��݃C���_�N�^���X��M�Ƃ���ƁA�R�ꎥ���������̂Ō����x���P�ƂȂ�
�l���P�~![]() �@[H]�ƂȂ�B
�@[H]�ƂȂ�B
L1�A�k2�̒l���������M��10-2�@[H]
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
| �ԍ� |
���� |
���� |
| 1 |
���C�͂Ɋւ���N�[�����̖@���i�^�j |  |
| 2 |
���ɂɂ�鎥�E�̋��� �i�^�j |
 |
| 3 |
���ɂɋy�ڂ��� |  |
| 4 |
���C���[�����g |  |
| 5 |
�r�I�E�T�o�[���̖@�� | 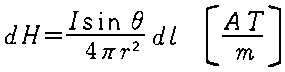 |
| 6 |
���������̂̂��̋����̎��E | 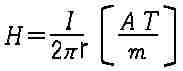 |
| 7 |
�~�`�R�C�����S�̎��E |  |
| 8 |
�������̃\���m�C�h���̎��E |  |
| 9 |
�N���� | 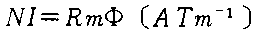 |
| 10 |
���� |  |
| 11 |
������ | 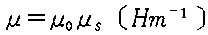 |
| 12 |
�������x | 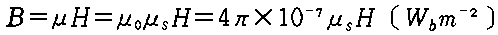 |
| 13 |
���C��R | 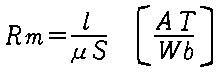 |
| 14 |
�d���� | 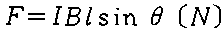 |
| 15 |
���s�d���Ԃ̗́i�^�j |  |
| 16 |
�����`�R�C���ɓ����g���N | 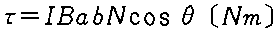 |
| 17 |
�d���͂ɂ��d�� | 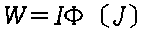 |
| 18 |
�U���N�d�� | 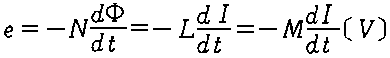 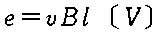 |
| 19 |
��\���m�C�h�̎��ȃC���_�N�^���X |  |
| 20 |
��\���m�C�h�̑��݃C���_�N�^���X | 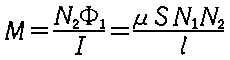  |
| 21 |
�d���G�l���M�[���x | 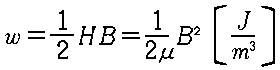 |
| 22 |
�C���_�N�^���X�̓d���G�l���M�[ |  |