(H11 電験3種機械)
定格電圧3 300[V]、定格電流210[A]の三相同期発電機がある。この発電機の電機子端子を開放した状態で界磁電流を増加していくと、120[A]に達したとき定格電圧が発生した。次に、その電機子端子を短絡して同じ120[A]の界磁を与えると、短絡電流は定格電流の1.4倍であった。この発電機の同期インピーダンス[Ω]の値として、正しいのは次のうちどれか。
[ ① 0.76 ② 1.6 ③ 3.7 ④ 6.5 ⑤ 11.2 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
題意より、同期発電機の相電圧は、線間電圧が3300(V)なので3300/![]() (V)、短絡電流は、定格電流の1.4倍なので、210×1.4
(V)、短絡電流は、定格電流の1.4倍なので、210×1.4
同期インピーダンスをZsとすると Zs=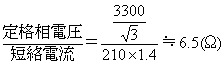
解答 ④
(H10 電験3種機械)
星形結線の非突極形三相同期発電機があり、各相の同期リアクタンスが3[Ω]、無負荷時の出力端子と中性点間の電圧が250[V]である。この発電機に純抵抗からなる三相平衡負荷を接続し、線電流50[A]を流したときの端子電圧[V]の値として、正しいのは次のうちどれか。ただし、電機子巻線抵抗は無視するものとする。
[ ① 173 ② 200 ③ 283 ④ 346 ⑤433 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
三相平衡負荷の1相の抵抗分をRとすると、線電流が50(A)、相電圧が250(V)、電源部のリアクタンスが3(Ω)ので、
![]()
求める端子電圧は線間電圧なので
![]() 解答 ④
解答 ④

(H10 電験3種機械)
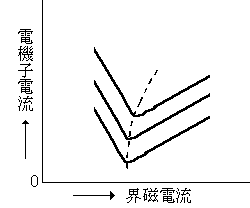
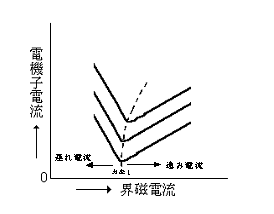
図は、同期電動機の電機子電流を縦軸に、界磁電流を横軸にとって、電機子電流と界磁電流を示したもので、これらの曲線は( ア )と呼ばれている。
これらの曲線には最低線が存在し、その点は( イ )に相当する。負荷が増大すると、この曲線は上方に移動し、最低点はある曲線を描いて変化する。最低点が描く曲線(破線)の右側の部分は( ウ )、左側の部分は( エ )の範囲である。
上記の記述中の空白箇所( ア )、( イ )、( ウ )及び( エ )に記入する字句として、正しいものを組み合わせたのは次のうちどれか。
( ア ) ( イ ) ( ウ ) ( エ )
① 速度特性曲線 最小速度 加 速 減 速
② 電流特性曲線 最小電流 遅れ電流 進み電流
③ 飽和特性電流 磁気飽和 負飽和 飽 和
④ 位相特性曲線 平衡点 増磁作用 減磁作用
⑤ 位相特性曲線 力率1 進み力率 遅れ力率
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
図は同期電動機の位相特性曲線(V曲線)であり、この曲線の最低点の箇所が力率=1の箇所である。電機子電流の少ない下に位置する曲線は軽負荷で、上部の曲線になるほど、重負荷の曲線となる。界磁電流の点線より左の部分が(電圧より)遅れ電流となり、右の部分が(電圧より)進み電流となる。
(H9 電験3種機械)
定格出力11 000[KVA]、定格電圧6 600[V]の三相同期発電機がある。三相短絡電流750[A]を流すのに必要な界磁電流が54[A]である場合、この発電機の定格電流に等しい三相短絡電流を流すのに必要な界磁電流[A]の値として、正しいのは次のうちどれか。
[ ① 69 ② 96 ③ 120 ④ 208 ⑤ 289 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
定格出力11 000[KVA]、定格電圧6 600[V]の三相同期発電機の定格電流をIとすると
I=![]()
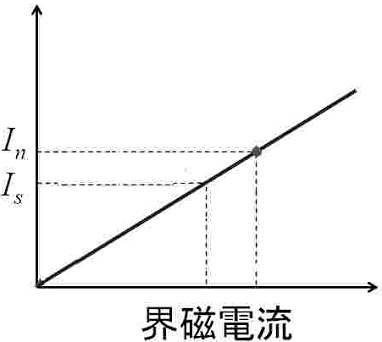
下図の三相同期発電機の三相短絡曲線のように、界磁電流と短絡電流は直線関係(比例関係)となる。三相短絡電流750[A]を流すのに必要な界磁電流が54[A]であるため、短絡電流962[A]を流すのに必要な界磁電流をXとすると、
750:54=962:X 750X=54×962 X=54×962÷750≒69 (A) 解答 ①
(H11 電験3種機械)
三相誘導電動機が滑り3[%]で運転している。このとき、電動機の二次銅損が147[W]であるとすると、電動機出力[kW]の値として、正しいのは次のうちどれか。ただし、機械損は無視するものとする。
[ ① 4.2 ② 4.5 ③ 4.8 ④ 5.1 ⑤ 5.4 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
三相誘導電動機の2次入力をP2、滑りをs、電動機出力をX,2次銅損をPsとすると、
Ps=sP2
X=(1-s)P2
上の2式より、![]()
題意よりPsが147W、sが0.03なので
X=147×0.97÷0.03=4735(W)≒4.8(kW) 解答 ③
(H10 電験3種機械)
定格周波数50[Hz]、4極の三相誘導電動機があり、トルク100[N・m]の負荷を負って1 440[r/min]で運転している。負荷トルクを50[N・m]に変更したときの電動機出力[kW]の値として、正しいのは次のうちどれか。ただし、電動機の滑りとトルクは比例するものとする。
[ ① 7.5 ② 7.7 ③ 7.9 ④ 74 ⑤ 79 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
f:周波数 p:極数の三相誘導電動機の同期速度Nは、
N=120×f/p
f=50[Hz] p=4極のときのNは、 N=120×50/4=1500 [r/min]
ゆえに、すべりsは、s=(1500-1440)/1500=0.04
題意より、電動機の滑りsとトルクτは比例するので、比例定数Aとすると
τ=Asが成立する。
トルク100[N・m]のときのすべりが0.04、負荷トルクを50[N・m]に変更したときの滑りをxとすると、
100=A×0.04・・・①
50=A×x ・・・②
②÷①より![]()
すべりが0.02のときの回転数は1500(1-0.02)=1470 [r/min]
このときの電動機出力をPとすると、P=τ×ω
τは50[N・m]、ωは2π×1470/60なので、
P=50×2π×1470/60=7697 (W) ≒7.7 (kW)
解答 ②
(H10 電験3種機械)
三相誘導電動機が一定電圧で運転中に周波数が下がると、回転速度は低下し、漏れリアクタンスは( ア )する。また、ギャップの磁束密度は( イ )し、励磁電流が増加して、力率が( ウ )する。
上記の記述中の空白の( ア )、( イ )及び( ウ )に記入する記号又は字句として、正しいものを組み合わせたのは次のうちどれか。
( ア ) ( イ ) ( ウ )
① 増大 減少 増大
② 減少 増大 減少
③ 増大 増大 減少
④ 減少 減少 増大
⑤ 増大 減少 減少
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
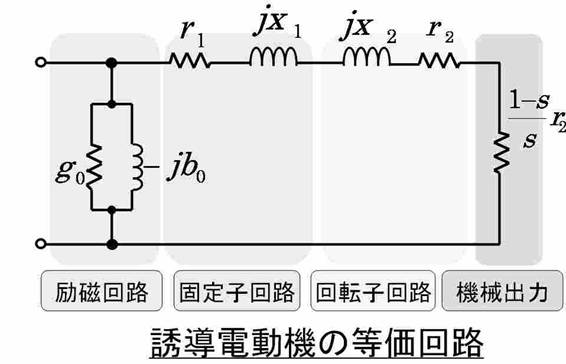
三相誘導電動機の等価回路を下図に示す。巻線の漏れリアクタンスであるjX1及びjX2は、ω(2πf)に比例する。つまり回転速度低下は、周波数fが小さくなることであり、結果として漏れリアクタンスが小さくなる。
また、電圧をE、磁束をφ、角速度をωとすると、E=Kφω(K:比例定数)が成り立つ。
そのため、φ∝E/ωとなり、供給電圧が一定であれば、磁束は周波数に反比例する。ゆえに回転速度が低下すると磁束は大きくなる。磁束は大きくなることは励磁電流が増加することであり、下図の等価回路より、励磁電流が増加すれば1次電流の力率が低下する。
解答 ②
(H9 電験3種機械)
定格出力200[kW]、定格電圧3 000[V]、周波数50[Hz]、8極のかご形三相誘導電動機がある。全負荷時の二次銅損は6[kW]、機械損は4[kW]である。この電動機の全負荷時の回転速度[rpm]として、正しいのは次のうちどれか。ただし、定格出力は定格負荷時の機械出力(発生動力)から機械損を引いたものに等しいものとする。
[ ① 714 ② 721 ③ 729 ④ 736 ⑤ 750 ]
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
★解答及び解説
定格出力200[kW]、全負荷時の二次銅損は6[kW]、機械損は4[kW]なので、2次入力をP2とすると、200+6+4=210 [kW]
三相誘導電動機の2次入力をP2、滑りをs、電動機出力をX,2次銅損をPsとすると、
次の関係式が成り立つ。
Ps=sP2・・・①
X=(1-s)P2
式①よりs=Ps/P2=6/210
周波数fが50[Hz]、極数pが8極の三相誘導電動機同期速度Nは、N=120×f/p
ゆえにN=120×50/8=750 [rpm]
全負荷時の滑りが6/210、定格回転数が750[rpm]なので、
回転数は、(1-6/210)×750≒729 [rpm] 解答 ③